第II卷
二.填空题:本大题共5小题,每小题5分,共25分.
11、11.已知两个单位向量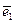 ,
,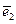 的夹角为
的夹角为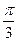 ,若向量
,若向量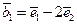 ,
,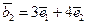 ,则
,则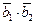 =___.
=___.
答案:-6. 解析:要求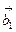 *
*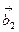 ,只需将题目已知条件带入,得:
,只需将题目已知条件带入,得:
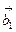 *
*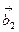 =(
=(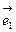 -2
-2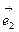 )*(3
)*(3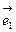 +4
+4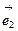 )=
)=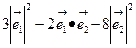
其中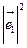 =1,
=1,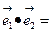 =
=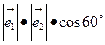 =1*1*
=1*1*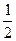 =
=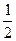 ,
,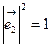 ,
,
带入,原式=3*1—2*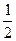 —8*1=—6
—8*1=—6
(PS: 这道题是道基础题,在我们做过的高考题中2007年广东文科的第四题,以及寒假题海班文科讲义73页的第十题,几乎是原题。考查的就是向量的基本运算。送分题(*^__^*) )
12.若双曲线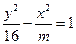 的离心率e=2,则m=____.
的离心率e=2,则m=____.
答案:48.解析:根据双曲线方程: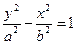 知,
知, 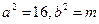 ,并在双曲线中有:
,并在双曲线中有: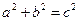 ,
,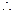 离心率e=
离心率e=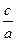 =2
=2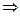
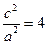 =
=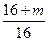 ,
,
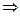 m=48
m=48
(PS: 这道题虽然考的是解析几何,大家印象中的解几题感觉都很难,但此题是个灰常轻松得分题(~ o ~)~zZ。你只需知道解几的一些基本定义,并且计算也不复杂。在2008年安徽文科的第14题以及2009福建文科的第4题,同时在我们寒假题海班讲义文科教材第145页的第3题,寒假理科教材第149页第30题都反复训练过。O(∩_∩)O。。所谓认真听课,勤做笔记,有的就是这个效果!!)
13.下图是某算法的程序框图,则程序运行后输出的结果是____.

答案:27. 解析:由框图的顺序,s=0,n=1,s=(s+n)n=(0+1)*1=1,n=n+1=2,依次循环
S=(1+2)*2=6,n=3,注意此刻3>3仍然是否,所以还要循环一次
s=(6+3)*3=27,n=4,此刻输出,s=27.
(PS: 程序框图的题一直是大家的青睐,就是一个循环计算的过程。2010天津文科卷的第3题,考题与此类似。在我们寒假文科讲义117页的第2题做过与此非常类似的,无非更改些数字。基础是关键!)
14.已知角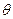 的顶点为坐标原点,始边为x轴的正半轴,若
的顶点为坐标原点,始边为x轴的正半轴,若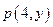 是角
是角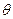 终边上一点,且
终边上一点,且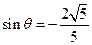 ,则y=_______.
,则y=_______.
答案:—8. 解析:根据正弦值为负数,判断角在第三、四象限,再加上横坐标为正,断定该角为第四象限角。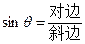 =
=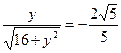
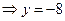
(PS:大家可以看到,步骤越来越少,不就意味着题也越来越简单吗?并且此题在我们春季班教材3第10页的第5题,出现了一模一样。怎么能说高考题是难题偏题。)
15.对于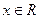 ,不等式
,不等式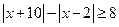 的解集为_______
的解集为_______
答案: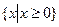 解析:两种方法,方法一:分三段,
解析:两种方法,方法一:分三段,
当x<-10时,-x-10+x-2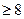 ,
, 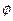
当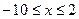 时,x+10-x+2
时,x+10-x+2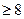 ,
,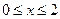
当x>2时, x+10-x+2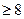 , x>2
, x>2
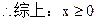
方法二:用绝对值的几何意义,可以看成到两点-10和2的距离差大于等于8的所有点的集合,画出数轴线,找到0到-10的距离为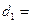 10,到2的距离为
10,到2的距离为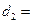 2,
2,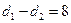 ,并当x往右移动,距离差会大于8,所以满足条件的x的范围是
,并当x往右移动,距离差会大于8,所以满足条件的x的范围是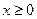 .
.
(PS: 此题竟出现在填空的最后一道压轴题,不知道神马情况。。。。。更加肯定考试考的都是基础,并且!!在我们除夕班的时候讲过一道一摸一样,只是换了数字而已的题型,在除夕教材第10页的15题。。太强悍啦!!几乎每道都是咱上课讲过的题目~~所以,亲爱的童鞋们,现在的你上课还在聊Q, 睡觉流口水吗??)
三.解答题:本大题共6小题,共75分.解答应写出文字说明、证明过程或演算步骤.
16.(本小题满分12分)
某饮料公司对一名员工进行测试以便确定其考评级别.公司准备了两种不同的饮料共5杯,其颜色完全相同,并且其中3杯为A饮料,另外2杯为B饮料,公司要求此员工一一品尝后,从5杯饮料中选出3杯A饮料.若该员工3杯都选对,则评为优秀;若3杯选对2杯,则评为良好;否则评为及格.假设此人对A和B两种饮料没有鉴别能力.
(1)求此人被评为优秀的概率;
(2)求此人被评为良好及以上的概率.
解:(1)员工选择的所有种类为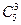 ,而3杯均选中共有
,而3杯均选中共有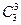 种,故概率为
种,故概率为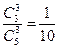 .
.
(2)员工选择的所有种类为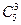 ,良好以上有两种可能:3杯均选中共有
,良好以上有两种可能:3杯均选中共有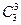 种;
种;
‚:3杯选中2杯共有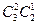 种。故概率为
种。故概率为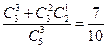 .
.
解析:本题考查的主要知识是排列组合与概率知识的结合,简单题。
17.(本小题满分12分)
在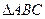 中,
中,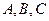 的对边分别是
的对边分别是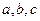 ,已知
,已知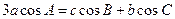 .
.
(1)求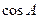 的值;
的值;
(2)若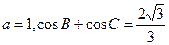 ,求边
,求边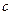 的值.
的值.
解:(1)由 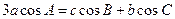 正弦定理得:
正弦定理得:
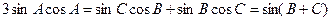
及: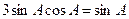 所以
所以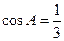 。
。
(2)由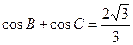
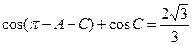 展开易得:
展开易得:
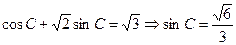
正弦定理: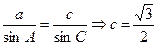
【解析】本题考查的主要知识三角函数及解三角形问题,题目偏难。第一问主要涉及到正弦定理、诱导公式及三角形内角和为180°这两个知识点的考查属于一般难度;第二问同样是对正弦定理和诱导公式的考查但形势更为复杂。












