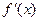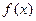18.(本小题满分12分)
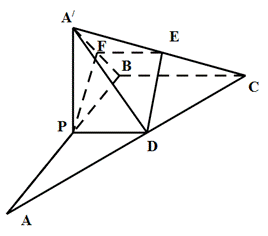
如图,在 交AC于 点D,现将
交AC于 点D,现将
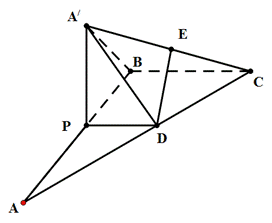
(1)当棱锥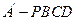 的体积最大时,求PA的长;
的体积最大时,求PA的长;
(2)若点P为AB的中点,E为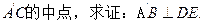
解(1)设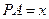 ,则
,则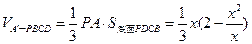
令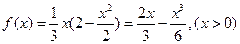
则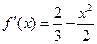
|
|
|
|
|
|
|
|
| 单调递增 | 极大值 | 单调递减 |
由上表易知:当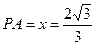 时,有
时,有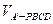 取最大值。
取最大值。
证明:
(2)作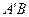 得中点F,连接EF、FP由已知得:
得中点F,连接EF、FP由已知得: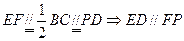
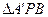 为等腰直角三角形,
为等腰直角三角形,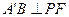 所以
所以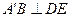 .
.
19.(本小题满分12分)
已知过抛物线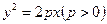 的焦点,斜率为
的焦点,斜率为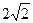 的直线交抛物线于
的直线交抛物线于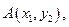
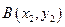 (
(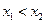 )两点,且
)两点,且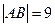 .
.
(1)求该抛物线的方程;
(2)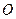 为坐标原点,
为坐标原点,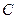 为抛物线上一点,若
为抛物线上一点,若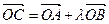 ,求
,求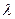 的值.
的值.
解析:(1)直线AB的方程是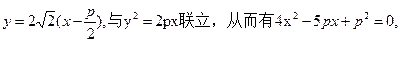
所以: ,由抛物线定义得:
,由抛物线定义得: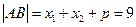 ,所以p=4,
,所以p=4,
抛物线方程为: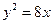
(2)、由p=4,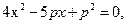 化简得
化简得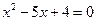 ,从而
,从而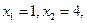
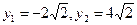 ,从而A:(1,
,从而A:(1,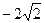 ),B(4,
),B(4,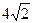 )
)
设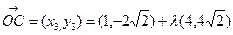 =
=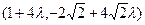 ,又
,又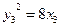 ,即
,即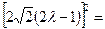 8(4
8(4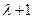 ),即
),即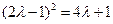 ,解得
,解得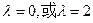
20.(本小题满分13分)
设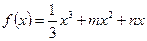 .
.
(1)如果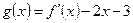 在
在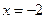 处取得最小值
处取得最小值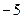 ,求
,求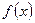 的解析式;
的解析式;
(2)如果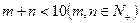 ,
,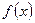 的单调递减区间的长度是正整数,试求
的单调递减区间的长度是正整数,试求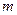 和
和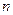
的值.(注:区间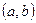 的长度为
的长度为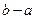 )
)
.解:(1)已知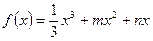 ,
,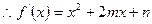
又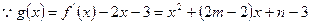 在
在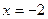 处取极值,
处取极值,
则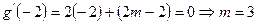 ,又在
,又在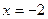 处取最小值-5.
处取最小值-5.
则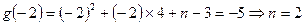
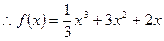
(2)要使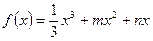 单调递减,则
单调递减,则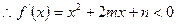
又递减区间长度是正整数,所以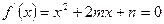 两根设做a,b。即有:
两根设做a,b。即有:
b-a为区间长度。又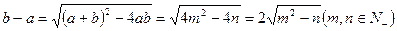
又b-a为正整数,且m+n<10,所以m=2,n=3或,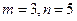 符合。
符合。
21.(本小题满分14分)
(1)已知两个等比数列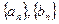 ,满足
,满足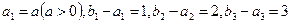 ,若数列
,若数列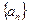 唯一,求
唯一,求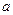 的值;
的值;
(2)是否存在两个等比数列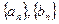 ,使得
,使得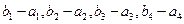 成公差
成公差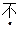 为
为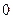 的等差数列?若存在,求
的等差数列?若存在,求 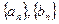 的通项公式;若
的通项公式;若 存在,说明理由.
存在,说明理由.
解:(1)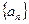 要唯一,
要唯一, 当公比
当公比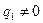 时,由
时,由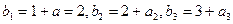 且
且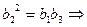
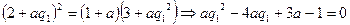 ,
,
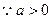 ,
,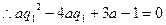 最少有一个根(有两个根时,保证仅有一个正根)
最少有一个根(有两个根时,保证仅有一个正根)
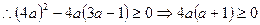 ,此时满足条件的a有无数多个,不符合。
,此时满足条件的a有无数多个,不符合。
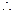 当公比
当公比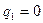 时,等比数列
时,等比数列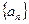 首项为a,其余各项均为常数0,唯一,此时由
首项为a,其余各项均为常数0,唯一,此时由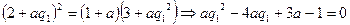 ,可推得
,可推得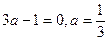 符合
符合
综上: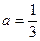 。
。
(2)假设存在这样的等比数列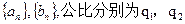 ,则由等差数列的性质可得:
,则由等差数列的性质可得: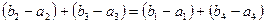 ,整理得:
,整理得: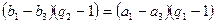
要使该式成立,则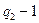 =
=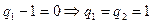 或
或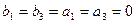 此时数列
此时数列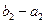 ,
,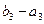 公差为0与题意不符,所以不存在这样的等比数列
公差为0与题意不符,所以不存在这样的等比数列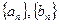 。
。