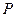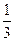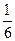三.解答题:本大题共小题,共74分.解答应写出文字说明、证明过程或演算步骤.
17.(本小题满分12分)
已知函数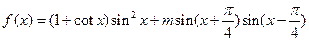 .
.
(1)当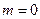 时,求
时,求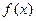 在区间
在区间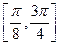 上的取值范围;
上的取值范围;
(2)当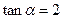 时,
时,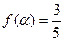 ,求
,求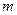 的值.
的值.
【命题意图】本题考查了两角和与差的三角函数,三角恒等变换,研究三角函数的性质以及三角函数在闭区间上的最值问题,方程思想求参数的值.考查了考生综合运用三角函数知识的解题能力.
【参考答案】(本小题满分12分)
解:(1)当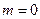 时,
时,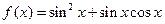
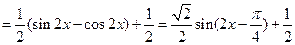
又由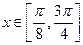 得
得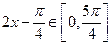 ,所以
,所以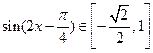 ,
,
从而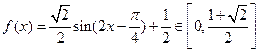 .
.
(2)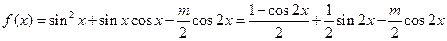
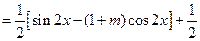
由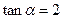 得
得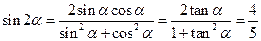 ,
,
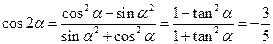 ,
,
所以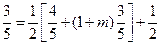 ,得
,得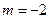 .
.
【点评】三角函数的定义和性质有着十分鲜明的特征和规律性,它和代数、几何有着密切的联系,是研究其他部分知识的工具,在实际问题中也有着广泛的应用,因而是高考对基础知识和基本技能考查的重要内容之一.有关三角函数的试题,其解题特点往往是先进行三角恒等变形,再利用三角函数的图象和性质解题,是高考的热点.
18.(本小题满分12分)
某迷宫有三个通道,进入迷宫的每个人都要经过一扇智能门.首次到达此门,系统会随机(即等可能)为你打开一个通道.若是1号通道,则需要1小时走出迷宫;若是2号、3号通道,则分别需要2小时、3小时返回智能门.再次到达智能门时,系统会随机打开一个你未到过的通道,直至走出迷宫为止.令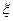 表示走出迷宫所需的时间.
表示走出迷宫所需的时间.
(1)求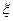 的分布列;(2)求
的分布列;(2)求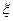 的数学期望.
的数学期望.
【命题意图】本题考查了相互独立事件同时发生的概率、考查了离散型随机变量的分布列以及数学期望的知识,考查了考生利用所学知识解决实际 问题的能力.
问题的能力.
【参考答案】(本小题满分12分)
解:(1)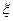 的所有可能取值为:1,3,4,6
的所有可能取值为:1,3,4,6
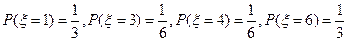 ,所以
,所以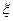 的分布列为:
的分布列为:
| 1 | 3 | 4 | 6 |
|
|
|
|
|
(2)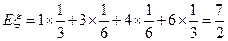 (小时)
(小时)
【点评】求离散型随机变量分布列和期望时要注意两个问题:一是求出随机变量所有可能的值;二是求出取每一个值时的概率.求随机变量的分布列,关键是概率类型的确定与转化.概率题目特点是与实际生活密切相关,应立足基础知识和基本方法的复习,抓好变式训练,从不同角度,不同侧面对题目进行分析,查找思维的缺陷,提高分析问题和解决实际问题的能力.
19.(本小题满分12分)
设函数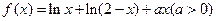 .
.
(1)当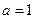 时,求
时,求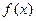 的单调区间;
的单调区间;
(2)若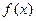 在
在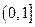 上的最大值为
上的最大值为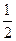 ,求
,求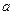 的值.
的值.
【命题意图】本题考查了利用导数研究函数的单调性、求函数的最值问题,考查了学生分析问题、解决问题的能力.

【点评】导数是初等数学与高等数学的重要衔接点,是对函数图象和性质的总结和拓展,是研究函数的单调性、极值、最值、讨论函数图象变化趋势的重要工具,利用导数可以解决现实生活中的最优化问题,由于其应用广泛性,已成为高考命题的重点和热点。以函数为背景,以导数为工具命题趋势,已成为高考的热点问题.
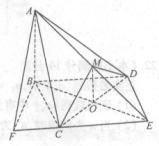
20.(本小题满分12分)
如图,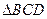 与
与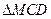 都是边长为2的正三角形,平面
都是边长为2的正三角形,平面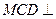 平面
平面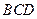 ,
,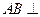 平面BCD,
平面BCD,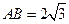 .
.
(1)求点A到平面MBC的距离;
(2)求平面ACM与平面BCD所成二面角的正弦值.
【命题意图】本题主要考查了空间几何体的线面关系、点到面的距离的求解以及二面角大小计算等问题,考查了考生的空间想象能力以及计算能力.
【参考答案】(本小题满分12分)
解法一:(1)取CD中点O,连OB,OM,
则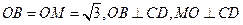 .
.
又平面MCD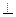 平面BCD,则MO
平面BCD,则MO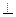 平面BCD,所以MO//AB,
平面BCD,所以MO//AB,
MO//平面ABC.M,O到平面ABC的距离相等.
作OH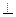 BC于H,连MH,则MH
BC于H,连MH,则MH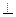 BC.
BC.
求得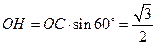 ,
,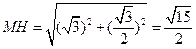 .
.
设点A到平面MB C的距离为
C的距离为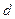 ,由
,由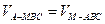 得
得
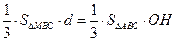 .
.
即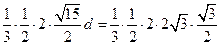 ,解得
,解得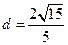 .
.

(1)设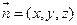 是平面MBC的法向量,则
是平面MBC的法向量,则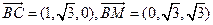 .
.
由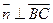 得
得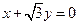 ;由
;由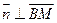 得
得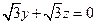 .
.
取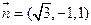 .
.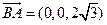 ,则
,则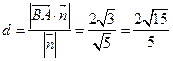 .
.
(2)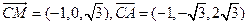 .
.
设平面ACM的法向量为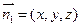 ,由
,由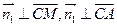 得
得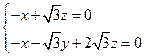 解得
解得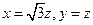 ,取
,取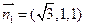 .
.
又平面BCD的法向量为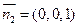 .所以
.所以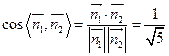 .
.
设所求二 面角为
面角为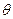 ,则
,则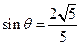 .
.
【点评】空间几何问题通常 包括点、线、面的位置关系的判断与证明以及点、线、面之间的角度或长度求解等问题,一般可以通过辅助线的构造,结合点、线、面的相应概念、性质、定理判断与求解.纵观近几年的高考试
包括点、线、面的位置关系的判断与证明以及点、线、面之间的角度或长度求解等问题,一般可以通过辅助线的构造,结合点、线、面的相应概念、性质、定理判断与求解.纵观近几年的高考试 题,立体几何的解答题在很大程度上扮演着直线与平面内容载体的角色,着重考查立体几何中的逻辑推理,多为中档题,通过这些题目考查考生掌握基础知识、逻辑推理能力、计算能力和空间想象能力.
题,立体几何的解答题在很大程度上扮演着直线与平面内容载体的角色,着重考查立体几何中的逻辑推理,多为中档题,通过这些题目考查考生掌握基础知识、逻辑推理能力、计算能力和空间想象能力.
21.(本小题满分12分)
设椭圆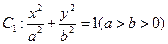 ,抛物线
,抛物线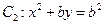 .
.
(1)若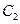 经过
经过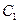 的两个焦点,求
的两个焦点,求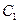 的离心率;(2)设
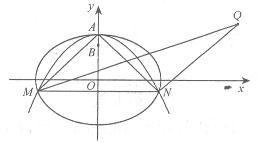
的离心率;(2)设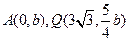 ,又M、N为
,又M、N为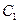 与
与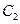 不在
不在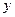 轴上的两个交点,若
轴上的两个交点,若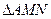 得垂心为
得垂心为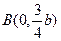 ,且
,且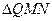 的重心在
的重心在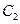 上,求椭圆
上,求椭圆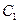 和抛物
和抛物 线
线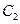 的方程.
的方程.
【命题意图】本题考查了椭圆的标准方程、、离心率、抛物线的标准方程及利用二者之间的位置关系,挖掘参数符合的条件等式,化简整理,从而求出方程.是一道综合性的试题,考查了学生综合运用知识分析推理直至解决问题的能力.
【参考答案】(本小题满分12分)
解:
(1)因为抛物线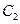 经过椭圆
经过椭圆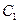 的两个焦点
的两个焦点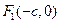 ,
,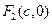 ,可得
,可得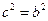 ,由
,由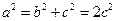 ,有
,有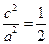 ,所以椭圆
,所以椭圆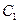 的离心率
的离心率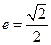 .
.
(2)由题设可知M,N关于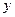 轴对称,设
轴对称,设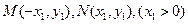 ,则由
,则由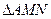 的垂心为B,有
的垂心为B,有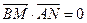 ,所以
,所以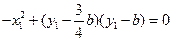
……①
由于点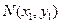 在
在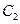 上,故有
上,故有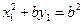 ……②
……②

【点评】解决此类问题时既要利用圆锥曲线的概念、性质,又要结合图形,利用平面几何三角形的重心,垂心的性质.一般考虑通过尽量多地消去未知数,简化已知条件来解决问题.
22.(本小题满分14分)
证明以下命题:
(1)对任一正整数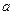 ,都存在正整数
,都存在正整数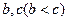 ,使得
,使得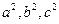 成等差数列;
成等差数列;
(2)存在无穷多个互不相似的三角形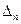 ,其边长
,其边长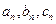 为正整数且
为正整数且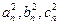 成等差数列.
成等差数列.
【命题意图】本题考查了等差数列的性质,考查了考生灵活运用所学知识解决问题的能力.是一道值得推敲的好题.
【参考答案】(本小题满分14分)
证明:
(1)易知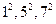 成等差数列,则
成等差数列,则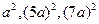 也成等差数列,所以对任一正整数
也成等差数列,所以对任一正整数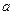 ,都存在正整数
,都存在正整数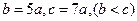 ,使得
,使得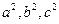 成等差数列.
成等差数列.
(2)若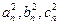 成等差数列,则有
成等差数列,则有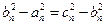 ,
,
即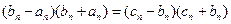 ……①
……①
选取关于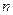 的一个多项式,例如
的一个多项式,例如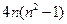 ,使得它可按两种方式分解因式,由于
,使得它可按两种方式分解因式,由于
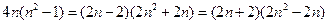
因此令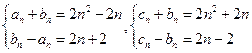 ,可得
,可得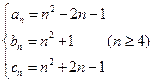
易验证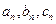 满足①,因此
满足①,因此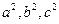 成等差数列,
成等差数列,
当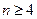 时,有
时,有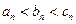 且
且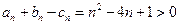
因此以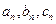 为边长可以构成三角形,
为边长可以构成三角形, 将此三角形记为
将此三角形记为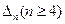 .
.
其次, 任取正整数
任取正整数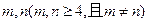 ,假若三角形
,假若三角形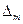 与
与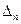 相似,则有:
相似,则有:
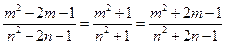
据此例性质有:
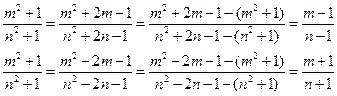
所以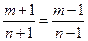 ,由此可得
,由此可得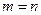 ,与假设
,与假设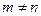 矛盾,即任两个三角形
矛盾,即任两个三角形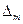 与
与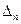
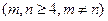 互不相似,所以存在无穷多个互不相似的三角形
互不相似,所以存在无穷多个互不相似的三角形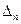 ,其边长
,其边长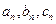 为正整数且以
为正整数且以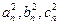 成等差数列.
成等差数列.
【点评】求解有关数列的综合题,首先要善于从宏观上整体把握问题,能透过给定信息的表象,揭示问题的本质,然后在微观上要明确解题方向,化难为易,化繁为简,注意解题的严谨性.数列问题对能力要求较高,特别是运算能力、归纳、猜想能力、转化能力、逻辑推理能力更为突出.而解答题更是考查能力的集中体现,尤其近几年高考加强了数列推理能力的考查,应引起我们足够的重视,因此,在平时要加强对能力的培养.