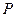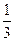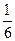(2
(2 )
)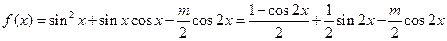
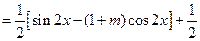
由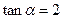 得
得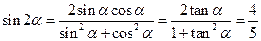 ,
,
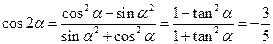 ,
,
所以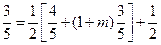 ,得
,得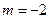 .
.
18.(本小题满分12分)
解:(1)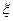 的所有可能取值为:1,3,4,6
的所有可能取值为:1,3,4,6
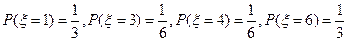 ,所以
,所以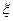 的分布列为:
的分布列为:
| 1 | 3 | 4 | 6 |
|
|
|
|
|
(2)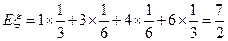 (小时)
(小时)
19.(本小题满分12分)
解:函数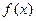 的定义域为
的定义域为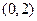 ,
,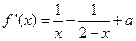 ,
,
(1)当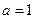 时,
时,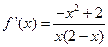 ,所以
,所以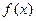 的单调递增区间为
的单调递增区间为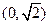 ,单调递减区间为
,单调递减区间为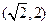 ;
;
(2)当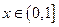 时,
时,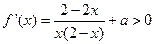 ,即
,即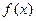 在
在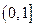 上单调递增,故
上单调递增,故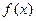 在
在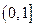 上的最大值为
上的最大值为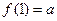 ,因此
,因此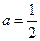 .
.
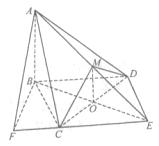
20.(本小题满分12分)
解法一:(1)取CD中点O,连OB,OM,
则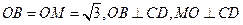 .
.
又平面MCD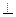 平面BCD,则MO
平面BCD,则MO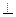 平面BCD,所以MO//AB,
平面BCD,所以MO//AB,
MO//平面ABC.M,O到平面ABC的距离相等.
作OH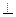 BC于H,连MH,则MH
BC于H,连MH,则MH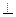 BC.
BC.
求得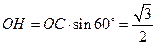 ,
,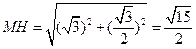 .
.
设点A到平面MBC的距离为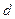 ,由
,由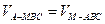 得
得
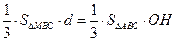 .
.
即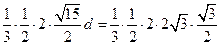 ,解得
,解得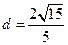 .
.
(2)延长AM、BO相交于E,连CE、DE,CE是平面ACM与平面BCD的交线.
由(1)知,O是BE的中点,则四边形BCED是棱形.
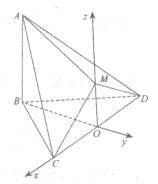
作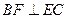 于F,连AF,则
于F,连AF,则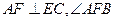 就是二面角
就是二面角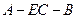 的平面角,设为
的平面角,设为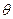 .
.
因为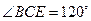 ,所以
,所以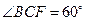 .
.
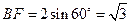 ,
,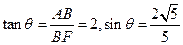 .
.
解法二:取CD中点O,连OB,OM,则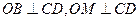 .又平面
.又平面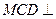 平面BCD,则
平面BCD,则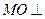 平面BCD.取O为原点,直线OC、BO、OM为
平面BCD.取O为原点,直线OC、BO、OM为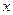 轴、
轴、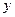 轴、
轴、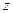 轴,建立空间直角坐标系如图.
轴,建立空间直角坐标系如图.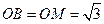 ,则各点坐标分别为
,则各点坐标分别为
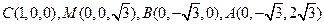 .
.
(1)设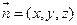 是平面MBC的法向量,则
是平面MBC的法向量,则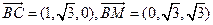 .
.
由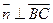 得
得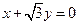 ;由
;由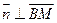 得
得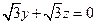 .
.
取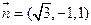 .
.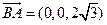 ,则
,则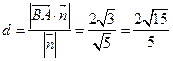 .
.
(2)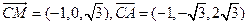 .
.
 设平面ACM的法向量为
设平面ACM的法向量为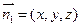 ,由
,由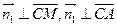 得
得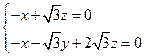 解得
解得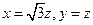 ,取
,取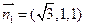 .
.
又平面BCD的法向量为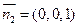 .所以
.所以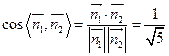 .
.
设所求二面角为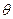 ,则
,则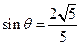 .
.

由①②得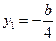 ,或
,或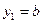 (舍去),
(舍去),
所以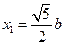 ,故
,故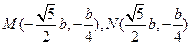 ,
,
所以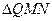 的重心为
的重心为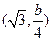 ,
,
因重心在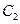 上得:
上得: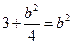 ,所以
,所以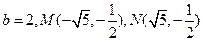 ,
,
又因为M,N在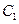 上,所以
上,所以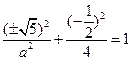 ,得
,得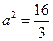 .
.
所以椭圆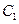 的方程为:
的方程为: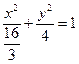 ,抛物线
,抛物线 的方程为:
的方程为: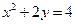 .
.
22.(本小题满分14分)
证明:
(1)易知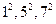 成等差数列,则
成等差数列,则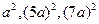 也成等差数列,所以对任一正整数
也成等差数列,所以对任一正整数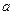 ,都存在正整数
,都存在正整数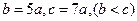 ,使得
,使得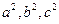 成等差数列.
成等差数列.
(2)若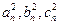 成等差数列,则有
成等差数列,则有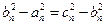 ,
,
即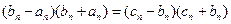 ……①
……①
选取关于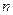 的一个多项式,例如
的一个多项式,例如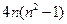 ,使得它可按两种方式分解因式,由于
,使得它可按两种方式分解因式,由于
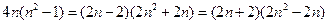
因此令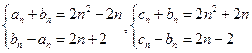 ,可得
,可得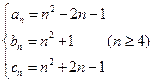
易验证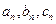 满足①,因此
满足①,因此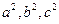 成等差数列,
成等差数列,
当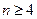 时,有
时,有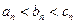 且
且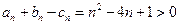
因此以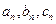 为边长可以构成三角形,将此三角形记为
为边长可以构成三角形,将此三角形记为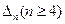 .
.
其次,任取正整数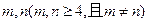 ,假若三角形
,假若三角形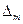 与
与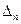 相似,则有:
相似,则有: