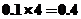一、选择题:本大题共10小题,每小题5分,共50分,在每小题给出的四个选项中,只有一项是符合要求的。
1.若向量a=(1,1),b=(-1,1),c=(4,2),则c=
A.3a+b B. 3a-b C.-a+3b D. a+3b
【答案】B
【解析】由计算可得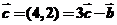 故选B
故选B
2.函数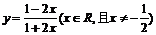 的反函数是
的反函数是
A.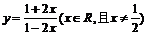 B.
B.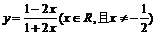
C.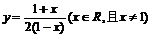 D.
D.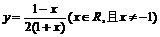
【答案】D
【解析】可反解得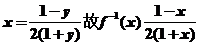 且可得原函数中y∈R、y≠-1所以
且可得原函数中y∈R、y≠-1所以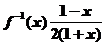 且x∈R、x≠-1选D
且x∈R、x≠-1选D
3.“sin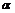 =
=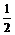 ”是“
”是“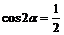 ”
” 的
的
A.充分而不必要条件 B.必要而不充分条件
C.充要条件 D.既不充分也不必要条件
【答案】A
【解析】由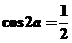 可得
可得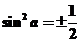 ,故
,故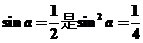 成立的充分不必要条件,故选A.
成立的充分不必要条件,故选A.
4.从5名志愿者中选派4人在星期五、星期六、星期日参加公益活动,每人一天,要求星期五有一人参加,星期六有两人参加,星期日有一人参加,则不同的选派方法共有
A.120种 B.96种 C.60种 D.48种
【答案】C
【解析】5人中选4人则有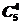 种,周五一人有
种,周五一人有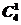 种,周六两人则有
种,周六两人则有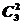 ,周日则有
,周日则有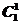 种,故共有
种,故共有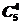 ×
×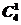 ×
×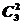 =60种,故选C
=60种,故选C
5.已知双曲线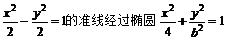 (b>0)的焦点,则b=
(b>0)的焦点,则b=
A.3 B.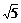 C.
C.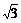 D.
D.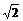

【答案】C
【解析】可得双曲线的准线为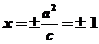 ,又因为椭圆焦点为
,又因为椭圆焦点为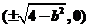 所以有
所以有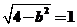 .即b2=3故b=
.即b2=3故b=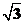 .故C.
.故C.
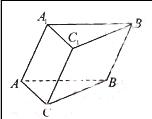
6.如图,在三棱柱ABC-A1B1C1中,∠ACB=900,∠ACC1=600,∠BCC1=450,侧棱CC1的长为1,则该三棱柱的高等于
A.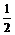 B.
B.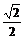
C.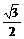
 D.
D.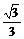
【答案】A
【解析】过顶点A作底面ABC的垂线,由已知条件和立体几何线面关系易求得高的长.
7.函数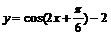 的图像F按向量a平移到F/,F/的解析式y=f(x),当y=f(x)为奇函数时,向量a可以等于
的图像F按向量a平移到F/,F/的解析式y=f(x),当y=f(x)为奇函数时,向量a可以等于
A.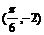 B.
B.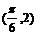 C.
C.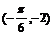 D.
D.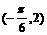
【答案】D
【解析】由平面向量平行规律可知,仅当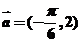 时,
时,
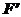 :
: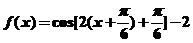 =
=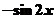 为奇函数,故选D.
为奇函数,故选D.
8.在“家电下乡”活动中,某厂要将100台洗衣机运往邻近的乡镇,现有4辆甲型货车和8辆乙型货车可供使用,每辆甲型货车运输费用400元,可装洗衣机20台;每辆乙型货车运输费用300元,可装洗衣机10台,若每辆至多只运一次,则该厂所花的最少运输费用为
A.2000元 B.2200元 C.2400元 D.2800元
【答案】B
【解析】设甲型货车使用x辆,已型货车y辆.则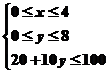 ,求Z=400x+300y最小值.可求出最优解为(4,2)故
,求Z=400x+300y最小值.可求出最优解为(4,2)故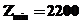 故选B.
故选B.
9.设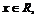 记不超过
记不超过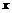 的最大整数为[
的最大整数为[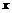 ],令{
],令{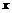 }=
}=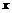 -[
-[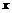 ],则
],则 {
{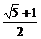 },[
},[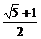 ],
],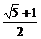
A.是等差数列但不是等比数列 B.是等比数列但不是等差数列
C.既是等差数列又是等比数列 D.既不是等差数列也不是等比数列
【答案】B
【解析】可分别求得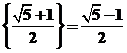 ,
,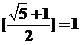 .则等比数列性质易得三者构成等比数列.
.则等比数列性质易得三者构成等比数列.
10.古希腊人常用小石子在沙滩上摆成各种性状来研究数,例如: 
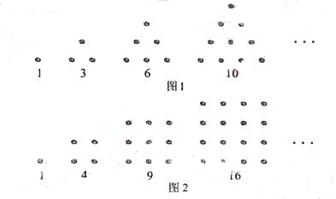
他们研究过图1中的1,3,6,10,…,由于这些数能够表示成三角形,将其称为三角形数;类似地,称图2中的1,4,9,16…这样的数成为正方形数。下列数中及时三角形数又是正方形数的是
A.289 B.1024 C.1225 D.1378
【答案】C
【解析】由图形可得三角形数构成的数列通项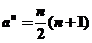 ,同理可得正方形数构成的数列通项
,同理可得正方形数构成的数列通项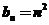 ,则由
,则由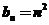
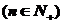 可排除A、D,又由
可排除A、D,又由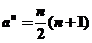 知
知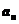 必为奇数,故选C.
必为奇数,故选C.
二.填空题:本大题共5小题,每小题5分,共25分。请将答案填在答题卡对应题号的位置上,一题两空的题,其答案按先后次序填写。
11 . 已知(1+ax)3,=1+10x+bx3+…+a3x3,则b= . 
【答案】40
【解析】因为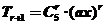 ∴
∴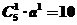
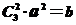 .解得
.解得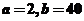
12. 甲、乙、丙三人将参加某项测试,他们能达标的概率分别是0.8、0.6、0.5,则三人都达标的概率是 ,三人中至少有一人达标的概率是 。
【答案】0.24 0.76
【解析】三人均达标为0.8×0.6×0.5=0.24,三人中至少有一人达标为1-0.24=0.76
13. 设集合A=(x∣log2x<1), B=(X∣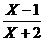 <1), 则A
<1), 则A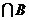 = .
= .
【答案】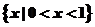
【解析】易得A=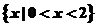 B=
B=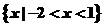 ∴A∩B=
∴A∩B=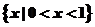 .
.
14. 过原点O作圆x2+y2‑-6x-8y+20=0的两条切线,设切点分别为P、Q,则线段PQ的长为 。
【答案】4
【解析】可得圆方程是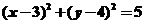 又由圆的切线性质及在三角形中运用正弦定理得
又由圆的切线性质及在三角形中运用正弦定理得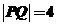
15. 下图是样本容量为200的频率分布直方图。
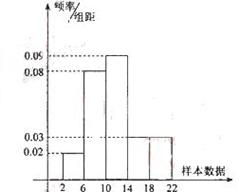
根据样本的频率分布直方图估计,样本数据落在【6,10】内的频数为 ,数据落在(2,10)内的概率约为 。
【答案】64
【解析】观察直方图易得频数为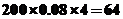 ,频率为
,频率为