三、解答题:本大题共6小题,共75分。解答应写出文字说明,证明过程或演算步骤。
16.(本小题满分12分)
在锐角△ABC中,a、b、c分别为角A、B、C所对的边,且
(Ⅰ)确定角C的大小:
(Ⅱ)若c=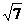 ,且△ABC的面积为
,且△ABC的面积为
 ,求a+b的值。
,求a+b的值。
解(1)由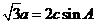 及正弦定理得,
及正弦定理得,
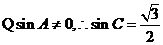
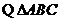 是锐角三角形,
是锐角三角形,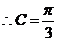
(2)解法1: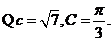 由面积公式得
由面积公式得
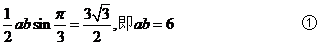
由余弦定理得
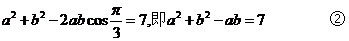
由②变形得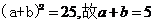
解法2:前同解法1,联立①、②得

消去b并整理得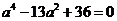 解得
解得
所以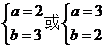 故
故
17. (本小题满分12分)
围建一个面积为360m2的矩形场地,要求矩形场地的一面利用旧墙(利用旧墙需维修),其它三面围墙要新建,在旧墙的对面的新墙上要留一个宽度为2m的进出口,如图所示,已知旧墙的维修费用为45元/m,新墙的造价为180元/m,设利用的旧墙的长度为x(单位:元)。
(Ⅰ)将y表示为x的函数:
(Ⅱ)试确定x,使修建此矩形场地围墙的总费用最小,并求出最小总费用。
17.解:(1)如图,设矩形的另一边长为a m
则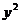 -45x-180(x-2)+180·2a=225x+360a-360
-45x-180(x-2)+180·2a=225x+360a-360
由已知xa=360,得a=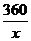 ,
,
所以y=225x+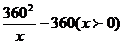
(II)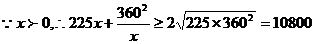

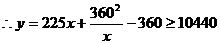 .当且仅当225x=
.当且仅当225x=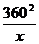 时,等号成立.
时,等号成立.
即当x=24m时,修建围墙的总费用最小,最小总费用是10440元.
18. (本小题满分12分)
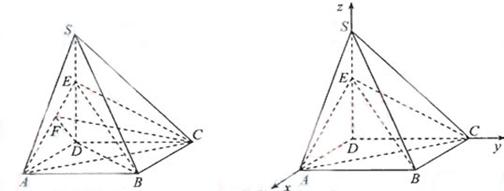
如图,四棱锥S=ABCD的底面是正方形,SD⊥平面ABCD,SD=AD=a,点E是SD上的点,且DE=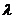 a(0<
a(0<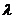 ≦1).
≦1).
(Ⅰ)求证:对任意的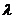
 (0、1),都有AC⊥BE:
(0、1),都有AC⊥BE:
(Ⅱ)若二面角C-AE-D的大小为600C,求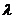 的值。
的值。
18. 本小题主要考察空间直线与直线、直线与平面的位置关系和二面角等基础知识,考查空间想象能力、推理论证能力和运算求解能力。(满分12分)
(Ⅰ)证发1:连接BD,由底面是正方形可得AC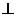 BD。
BD。
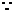 SD
SD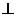 平面ABCD,
平面ABCD,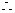 BD是BE在平面ABCD上的射影,
BD是BE在平面ABCD上的射影,
由三垂线定理得AC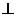 BE.
BE.
(II)解法1: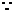 SD
SD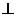 平面ABCD,CD
平面ABCD,CD 平面ABCD,
平面ABCD,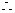 SD
SD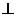 CD.
CD.
又底面ABCD是正方形,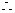 CD
CD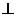 AD,又SD
AD,又SD AD=D,
AD=D,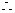 CD
CD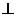 平面SAD。
平面SAD。
过点D在平面SAD内做DF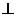 AE于F,连接CF,则CF
AE于F,连接CF,则CF AE,
AE,
故 CFD是二面角C-AE-D 的平面角,即
CFD是二面角C-AE-D 的平面角,即 CFD=60°
CFD=60°
在Rt△ADE中, AD=
AD=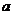 , DE=
, DE= 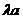 , AE=
, AE=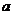
 。
。
于是,DF=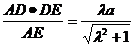
在Rt△CDF中,由 cot60°=
cot60°=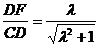
得 , 即
, 即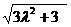 =3
=3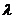
 , 解得
, 解得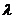 =
=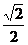
19.(本小题满分12分)
已知{an}是一个公差大于0的等差数列,且满足a3a6=55, a2+a7=16.
(Ⅰ)求数列{an}的通项公式:
(Ⅱ)若数列{an}和数列{bn}满足等式:an==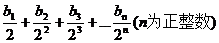 ,求数列{bn}的前n项和Sn
,求数列{bn}的前n项和Sn
解(1)解:设等差数列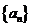 的公差为d,则依题设d>0
的公差为d,则依题设d>0
由a2+a7=16.得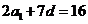 ①
①
由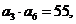 得
得 ②
②
由①得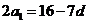 将其代入②得
将其代入②得 。即
。即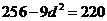
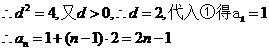

(2)令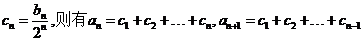
两式 相减得
相减得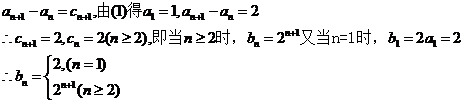
于是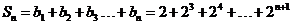
= -4=
-4=