20.(本小题满分13分)
如图,过抛物线y2=2PX(P>0)的焦点F的直线与抛物线相交于M、N两点,自M、N向准线L作垂线,垂足分别为M1、N1
(Ⅱ)记△FMM1、、△FM1N1、△FN N1的面积分别为S1、、S2、,S3,试判断S22=4S1S3是否成立,并证明你的结论。
20题。本小题主要考查抛物线的概念,抛物线的几何性质等平面解析几何的基础知识,考查综合运用数学知识进行推理运算的能力(满分13分)
(1) 证法1:由抛物线的定义得
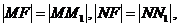
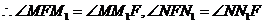 2分
2分
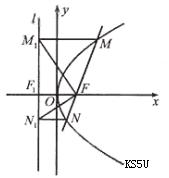 如图,设准线l与x的交点为
如图,设准线l与x的交点为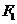

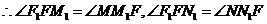
而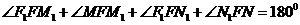
即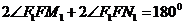

故
证法2:依题意,焦点为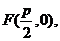 准线l的方程为
准线l的方程为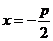
设点M,N的坐标分别为 直线MN的方程为
直线MN的方程为 ,则有
,则有

由 得
得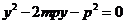
于是, ,
,
 ,故
,故
(Ⅱ) 成立,证明如下:
成立,证明如下:
证法1:设 ,则由抛物线的定义得
,则由抛物线的定义得
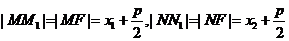 ,于是
,于是

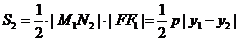
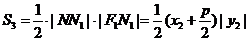

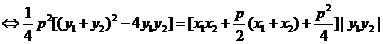
将 与
与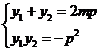 代入上式化简可得
代入上式化简可得 
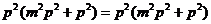 ,此式恒成立。
,此式恒成立。
故 成立。
成立。
证法2:如图,设直线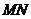 M的倾角为
M的倾角为 ,
,
则由抛物线的定义得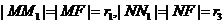

于是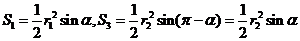
在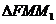 和
和 中,由余弦定理可得
中,由余弦定理可得

由(I)的结论,得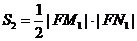

即 ,得证。
,得证。
21.(本小题满分14分)
已知关于x的函数f(x)=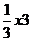 +bx2+cx+bc,其导函数为f+(x).令g(x)=∣f+(x) ∣,记函数g(x)在区间[-1、1]上的最大值为M.
+bx2+cx+bc,其导函数为f+(x).令g(x)=∣f+(x) ∣,记函数g(x)在区间[-1、1]上的最大值为M.
(Ⅰ)如果函数f(x)在x=1处有极值- ,试确定b、c的值:
,试确定b、c的值:
(Ⅱ)若∣b∣>1,证明对任意的c,都有M>2: 
(Ⅲ)若M≧K对任意的b、c恒成立,试求k的最大值。
21.本小题主要考察函数、函数的导数和不等式等基础知识,考察综合运用数学知识进行推理论证的能力和份额类讨论的思想(满分14分)
(I)解: ,由
,由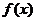 在
在 处有极值
处有极值
可得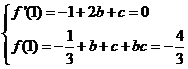
解得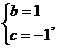 或
或
若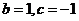 ,则
,则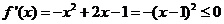 ,此时
,此时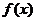 没有极值;
没有极值;
若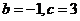 ,则
,则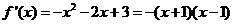
当 变化时,
变化时,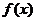 ,
,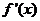 的变化情况如下表:
的变化情况如下表:
|
|
|
| 1 |
|
|
| 0 | + | 0 |
|
|
| 极小值 |
| 极大值 |
|
 当
当 时,
时,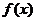 有极大值
有极大值 ,故
,故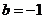 ,
, 即为所求。
即为所求。
(Ⅱ)证法1:
当 时,函数
时,函数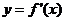 的对称轴
的对称轴 位于区间
位于区间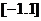 之外。
之外。
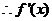 在
在 上的最值在两端点处取得
上的最值在两端点处取得
故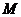 应是
应是 和
和 中较大的一个
中较大的一个
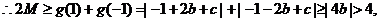 即
即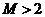
证法2(反证法):因为 ,所以函数
,所以函数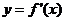 的对称轴
的对称轴 位于区间
位于区间 之外,
之外,
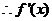 在
在 上的最值在两端点处取得。
上的最值在两端点处取得。
故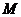 应是
应是 和
和 中较大的一个
中较大的一个
假设 ,则
,则
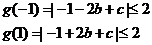
将上述两式相加得:
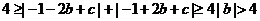 ,导致矛盾,
,导致矛盾,
(Ⅲ)解法1:
(1)当 时,由(Ⅱ)可知
时,由(Ⅱ)可知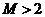 ;
;
(2)当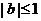 时,函数
时,函数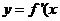 )的对称轴
)的对称轴 位于区间
位于区间 内,
内, 

此时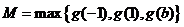
由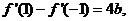 有
有
①若 则
则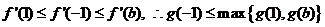 ,
,
于是
②若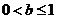 ,则
,则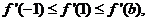

于是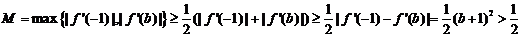
综上,对任意的 、
、 都有
都有
而当 时,
时, 在区间
在区间 上的最大值
上的最大值
故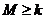 对任意的
对任意的 、
、 恒成立的
恒成立的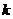 的最大值为
的最大值为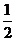 。
。
解法2:
(1)当 时,由(Ⅱ)可知
时,由(Ⅱ)可知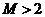 ;
; 
(2)当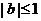 时,函数
时,函数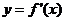 的对称轴
的对称轴 位于区间
位于区间 内,
内,
此时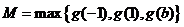

 ,即
,即
下同解法1