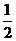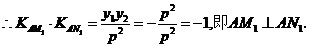三、解答题:本大题共6小题,共75分。解答应写出文字说明、证明过程或演算步骤。
16.(本小题满分10分)(注意:在试题卷上作答无效)
一个盒子里装有4张大小形状完全相同的卡片,分别标有数2,3,4,5;另一个盒子也装有4张大小形状完全相同的卡片,分别标有数3,4,5,6。现从一个盒子中任取一张卡片,其上面的数记为x;再从另一盒子里任取一张卡片,其上面的数记为y,记随机变量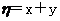 ,求
,求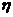 的分布列和数学期望。
的分布列和数学期望。
16.解析:依题意,可分别取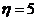 、6、
、6、 11取,则有
11取,则有
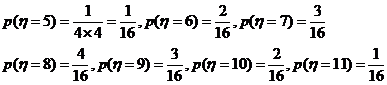
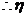 的分布列为
的分布列为
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
|
|
| |
|
|
|
|
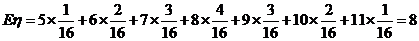 .
.
17.(本小题满分12分)(注意:在试题卷上作答无效)
已知向量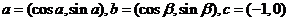
(Ⅰ)求向量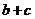 的长度的最大值;
的长度的最大值;
(Ⅱ)设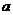
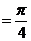 ,且
,且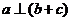 ,求
,求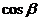 的值。
的值。
17.解析:(1)解法1: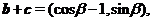 则
则
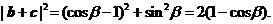
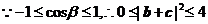 ,即
,即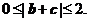

当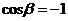 时,有
时,有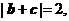 所以向量
所以向量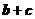 的长度的最大值为2.
的长度的最大值为2.
解法2: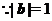 ,
,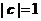 ,
,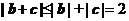
当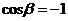 时,有
时,有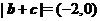 ,即
,即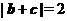 ,
,
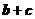 的长度的最大值为2.
的长度的最大值为2.
(2)解法1:由已知可得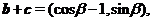
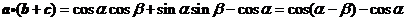 。
。
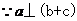 ,
,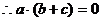 ,即
,即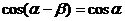 。
。
由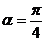 ,得
,得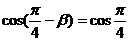 ,即
,即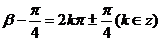 。
。
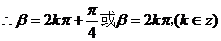 ,于是
,于是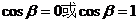 。
。
解法2:若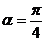 ,则
,则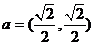 ,又由
,又由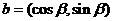 ,
,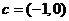 得
得
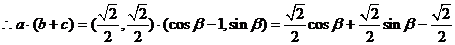
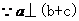 ,
,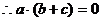 ,即
,即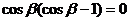
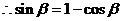 ,平方后化简得
,平方后化简得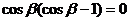

解得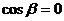 或
或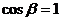 ,经检验,
,经检验,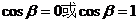 即为所求
即为所求
18.(本小题满分12分)(注意:在试题卷上作答无效)
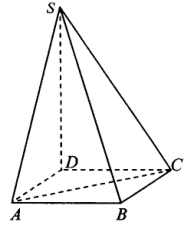
如图,四棱锥S—ABCD的底面是正方形,SD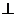 平面ABCD,SD=2a,
平面ABCD,SD=2a,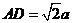 点E是SD上的点,且
点E是SD上的点,且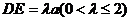
(Ⅰ)求证:对任意的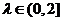 ,都有
,都有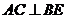
(Ⅱ)设二面角C—AE—D的大小为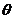
 ,直线BE与平面ABCD所成的角为
,直线BE与平面ABCD所成的角为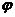 ,若
,若 ,求
,求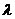 的值
的值 

18.(Ⅰ)证法1:如图1,连接BE、BD,由地面ABCD是正方形可得AC⊥BD。
 SD⊥平面ABCD,
SD⊥平面ABCD, BD是BE在平面ABCD上的射影,
BD是BE在平面ABCD上的射影, AC⊥BE
AC⊥BE
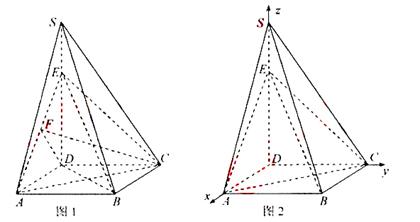
(Ⅱ)解法1:如图1,由SD⊥平面ABCD知,∠DBE= 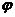 ,
,
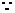 SD⊥平面ABCD,CD
SD⊥平面ABCD,CD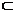 平面ABCD,
平面ABCD, 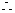 SD⊥CD。
SD⊥CD。
又底面ABCD是正方形,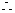 CD⊥AD,而SD
CD⊥AD,而SD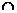 AD=D,CD⊥平面SAD.
AD=D,CD⊥平面SAD.
连接AE、CE,过点D在平面SAD内作DE⊥AE于F,连接CF,则CF⊥AE,
故∠CDF是二面角C-AE-D的平面角,即∠CDF=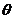 。
。
在Rt△BDE中,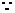 BD=2a,DE=
BD=2a,DE=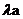
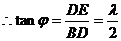
在Rt△ADE中, 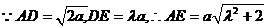
从而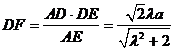
在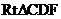 中,
中,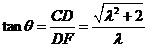 .
. 
由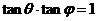 ,得
,得
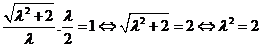 .
.
由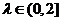 ,解得
,解得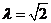 ,即为所求.
,即为所求.
(I) 证法2:以D为原点,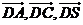 的方向分别作为x,y,z轴的正方向建立如
的方向分别作为x,y,z轴的正方向建立如
图2所示的空间直角坐标系,则
D(0,0,0),A(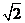 ,0,0),B(
,0,0),B(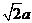 ,
,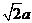 ,0),C(0,
,0),C(0,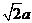 ,0),E(0,0
,0),E(0,0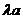 ),
),
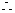
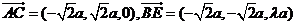
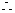
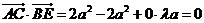 ,
,
即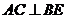 。
。
(II) 解法2:
由(I)得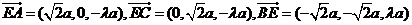 .
.
设平面ACE的法向量为n=(x,y,z),则由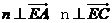 得
得

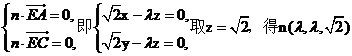 。
。
 易知平面ABCD与平面ADE的一个法向量分别为
易知平面ABCD与平面ADE的一个法向量分别为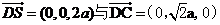 .
.
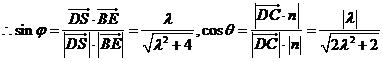 .
. 

 0<
0<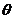 ,
,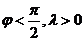 ,
,
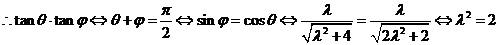 .
.
由于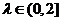 ,解得
,解得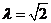 ,即为所求。
,即为所求。
[]
19、(本小题满分13分)(注意:在试题卷上作答无效)
已知数列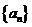 的前n项和
的前n项和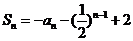 (n为正整数)。
(n为正整数)。
(Ⅰ)令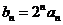 ,求证数列
,求证数列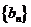 是等差数列,并求数列
是等差数列,并求数列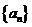 的通项公式;
的通项公式;
(Ⅱ)令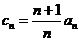 ,
,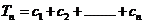 试比较
试比较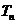 与
与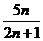 的大小,并予以证明。
的大小,并予以证明。
19.解析:(I)在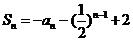 中,令n=1,可得
中,令n=1,可得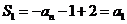 ,即
,即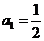
当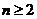 时,
时,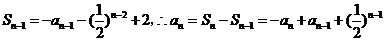 ,
,

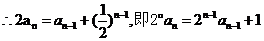 .
.
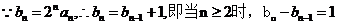 .
. 
又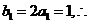 数列
数列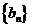 是首项和公差均为1的等差数列.
是首项和公差均为1的等差数列.
于是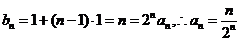 .
.
(II)由(I)得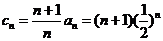 ,所以
,所以
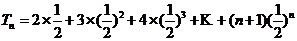
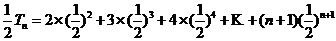
由①-②得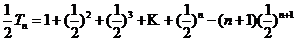


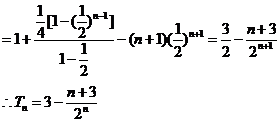
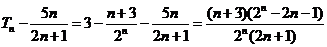
于是确定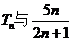 的大小关系等价于比较
的大小关系等价于比较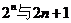 的大小
的大小
由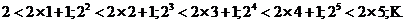


可猜想当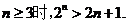 证明如下:
证明如下:
证法1:(1)当n=3时,由上验算显示成立。
(2)假设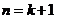 时
时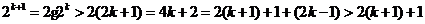
所以当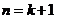 时猜想也成立
时猜想也成立
综合(1)(2)可知 ,对一切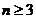 的正整数,都有
的正整数,都有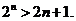
证法2:当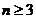 时
时
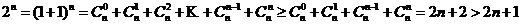
综上所述,当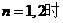
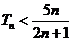 ,当
,当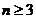 时
时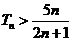
20、(本小题满分14分)(注意:在试题卷上作答无效)
过抛物线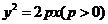 的对称轴上一点
的对称轴上一点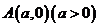 的直线与抛物线相交于M、N两点,自M、N向直线
的直线与抛物线相交于M、N两点,自M、N向直线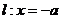 作垂线,垂足分别为
作垂线,垂足分别为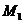 、
、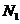 。
。
(Ⅰ)当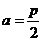 时,求证:
时,求证: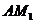 ⊥
⊥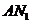 ;
;
(Ⅱ)记
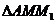 、
、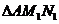 、
、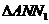 的面积分别为
的面积分别为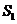 、
、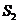 、
、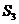 ,是否存在
,是否存在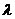 ,使得对任意的
,使得对任意的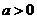 ,都有
,都有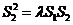 成立。若存在,求出
成立。若存在,求出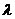 的值;若不存在,说明理由。
的值;若不存在,说明理由。
20题。本小题主要考察抛物线的定义和几何性质等平面解析几何的基础知识,考查综合运用数学知识进行推理运算的能力。(14分)
解:依题意,可设直线MN的方程为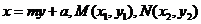 ,则有
,则有
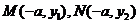
由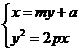 消去x可得
消去x可得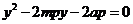

从而有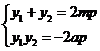 ①
①
于是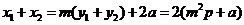 ②
②
又由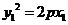 ,
,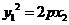 可得
可得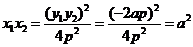 ③
③
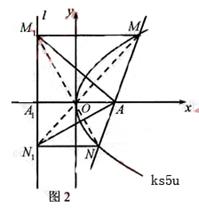
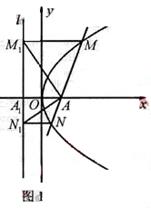
(Ⅰ)如图1,当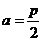 时,点
时,点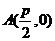 即为抛物线的焦点,
即为抛物线的焦点,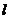 为其准线
为其准线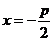
此时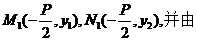 ①可得
①可得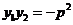
证法1: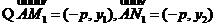
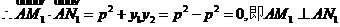
证法2:
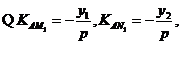
(Ⅱ)存在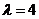 ,使得对任意的
,使得对任意的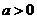 ,都有
,都有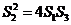 成立,证明如下:
成立,证明如下:
证法1:记直线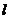 与x轴的交点为
与x轴的交点为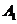 ,则
,则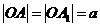 。于是有
。于是有
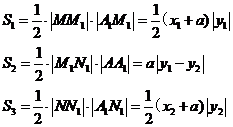
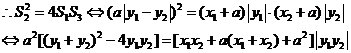
将①、②、③代入上式化简可得
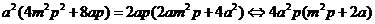
上式恒成立,即对任意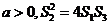 成立
成立
证法2:如图2,连接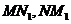 ,则由
,则由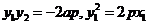 可得
可得
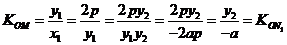 ,所以直线
,所以直线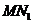 经过原点O,
经过原点O,
同理可证直线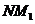 也经过原点O
也经过原点O
又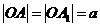 设
设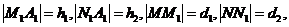 则
则
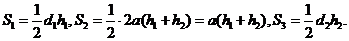
21.(本小题满分14分) (注意:在试题卷上作答无效)
在R上定义运算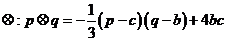 (b、c为实常数)。记
(b、c为实常数)。记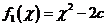 ,
,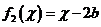 ,
,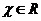 .令
.令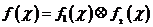 .
.
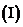 如果函数
如果函数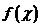 在
在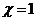 处有极什
处有极什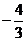 ,试确定b、c的值;
,试确定b、c的值;
 求曲线
求曲线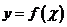 上斜率为c的切线与该曲线的公共点;
上斜率为c的切线与该曲线的公共点;
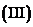 记
记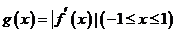 的最大值为
的最大值为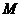 .若
.若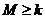 对任意的b、c恒成立,试示
对任意的b、c恒成立,试示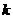 的最大值。
的最大值。
21题 当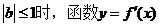 得对称轴x=b位于区间
得对称轴x=b位于区间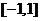 之外
之外
此时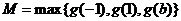
由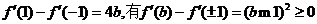
① 若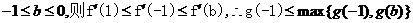
于是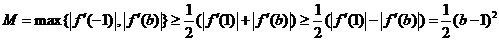
② 若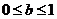 ,则
,则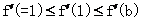 ,
,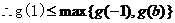
于是
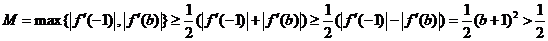
综上,对任意的b、c都有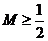
而当,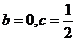 时,
时,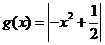 在区间
在区间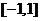 上的最大值
上的最大值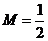
故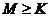 对任意的b,c恒成立的k的最大值为
对任意的b,c恒成立的k的最大值为