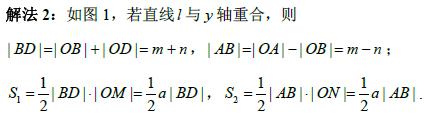20.(本小题满分13分)
如图,某地质队自水平地面A,B,C三处垂直向地下钻探,自A点向下钻到A1处发现矿藏,再继续下钻到A2处后下面已无矿,从而得到在A处正下方的矿层厚度为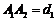 .同样可得在B,C处正下方的矿层厚度分别为
.同样可得在B,C处正下方的矿层厚度分别为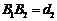 ,
,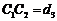 ,且
,且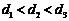 . 过
. 过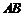 ,
,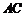 的中点
的中点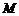 ,
,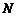 且与直线
且与直线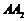 平行的平面截多面体
平行的平面截多面体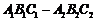 所得的截面
所得的截面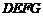 为该多面体的一个中截面,其面积记为
为该多面体的一个中截面,其面积记为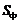 .
.
(Ⅰ)证明:中截面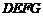 是梯形;
是梯形;
(Ⅱ)在△ABC中,记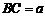 ,BC边上的高为
,BC边上的高为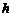 ,面积为
,面积为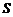 . 在估测三角形
. 在估测三角形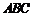 区域内正下方的矿藏储量(即多面体
区域内正下方的矿藏储量(即多面体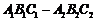 的体积
的体积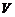 )时,可用近似公式
)时,可用近似公式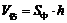 来估算. 已知
来估算. 已知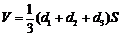 ,试判断
,试判断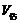 与V的大小关系,并加以证明.
与V的大小关系,并加以证明.




21.(本小题满分13分)
设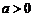 ,
,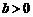 ,已知函数
,已知函数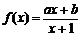 .
.
(Ⅰ)当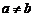 时,讨论函数
时,讨论函数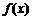 的单调性;
的单调性;
(Ⅱ)当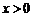 时,称
时,称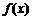 为
为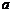 、
、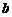 关于
关于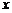 的加权平均数.
的加权平均数.
(i)判断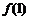 ,
, 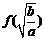 ,
,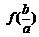 是否成等比数列,并证明
是否成等比数列,并证明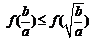 ;
;
(ii)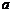 、
、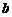 的几何平均数记为G. 称
的几何平均数记为G. 称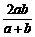 为
为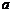 、
、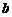 的调和平均数,记为H.
的调和平均数,记为H.
若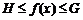 ,求
,求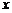 的取值范围.
的取值范围.

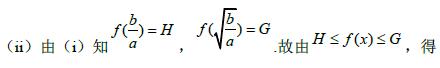


22.(本小题满分14分)
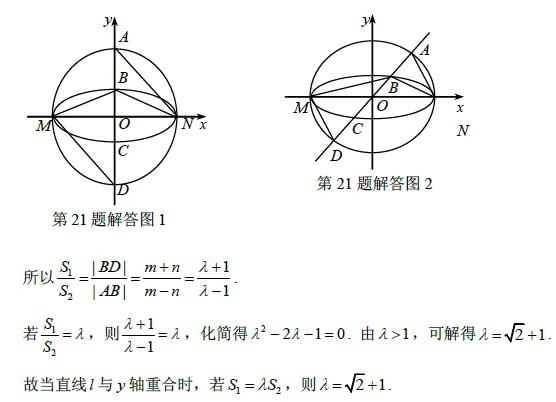
如图,已知椭圆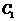 与
与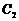 的中心在坐标原点
的中心在坐标原点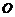 ,长轴均为
,长轴均为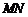 且在
且在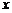 轴上,短轴长分别
轴上,短轴长分别
为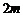 ,
,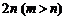 ,过原点且不与
,过原点且不与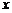 轴重合的直线
轴重合的直线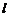 与
与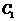 ,
,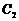 的四个交点按纵坐标从
的四个交点按纵坐标从
大到小依次为A,B,C,D.记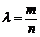 ,△
,△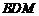 和△
和△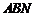 的面积分别为
的面积分别为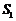 和
和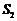 .
.
(Ⅰ)当直线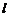 与
与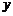 轴重合时,若
轴重合时,若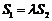 ,求
,求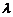 的值;
的值;
(Ⅱ)当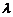 变化时,是否存在与坐标轴不重合的直线l,使得
变化时,是否存在与坐标轴不重合的直线l,使得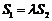 ?并说明理由.
?并说明理由.