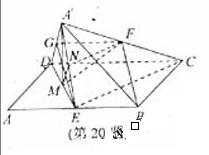
(20)(本题满分14分)如图,在平行四边形ABCD中,AB=2BC,∠ABC=120°,E为线段AB的中线,将△ADE沿直线DE翻折成△A′DE,使平面A′DE⊥平面BCD,F为线段A′C的中点.
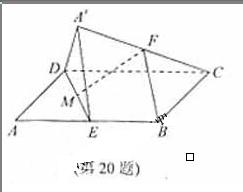
(Ⅰ)求证:BF∥平面A′DE;
(Ⅱ)设M为线段DE的中点,求直线FM与平面
A′DE所成角的余弦值.
【命题意图】本题主要考查空间线线、线面、面面位置关系,线面角等基础知识,同时考查空间想象能力和推理论证能力.
【答案】
(Ⅰ)证明:取A′D的中点G,连结GF,CE,由条件易知
FG∥CD,FG=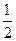 CD.
CD.
BE∥CD,BE=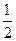 CD.
CD.
所以FG∥BE,FG=BE.
故四边形BEGF为平行四边形,
所以BF∥EG
 因为
因为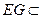 平面A′DE,BF
平面A′DE,BF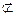 平面A′DE.
平面A′DE.
所以BF//平面A′DE.
(Ⅱ)解:在平行四边形ABCD中,设BC =a,
=a,
则AB=CD=2a,AD=AE=EB=a,
连CE.
因为∠ABC=120°,
在△BCE中,可得CE=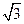 a,
a,
在△ADE中,可得DE=a,
在△CDE中,因为CD2=CE2+DE2,所以CE⊥DE,
在正三角形A′DE中,M为DE中点,所以A′M⊥DE.
由平面A′DE⊥平面BCD,
可知A′M⊥平面BCD,A′M⊥CE.
取A′E的中点N,连线NM、NF,
所以NF⊥DE,NF⊥A′M.
因为DE交A′M于M,
所 以NF⊥平面A′DE,
以NF⊥平面A′DE,
则∠FMN为直线FM与平面A′DE新成角.
在Rt△FMN中,NF=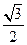 a, MN=
a, MN=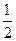 a, FM=a,
a, FM=a,
则cos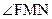 =
=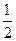 .
.
所以直线FM与平面A′DE所成角的余弦值为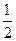 .
.
【点评】空间角的计算方法都是转化为平面角来计算的,直线与平面所成的角是平面的一条斜线和它在平面上的射影所成的锐角(直线与平面垂直或平行包括直线在平面内事,成直角或0°角,我们往往在斜线上取一点向平面引垂线,以形成由平面的斜线、垂线及斜线在平面上的射影组成的直角三角形,这里的关键是引平面的垂线.
(21)(本题满分15分)已知函数f(x)=(x-a)2(x-b)(a,b∈R,a<b).
(Ⅰ)当a=1,b=2时,求曲线y=f(x)在点(2,f(2))处的切线方程;
(Ⅱ)设x1,x2是f(x)的两个极值点,x3是f(x)的一个零点,且x3≠x1,x3≠x2.
证明:存在实数x4,使得x1,x2,x3,x4按某种顺序排列后构成等差数列,并求x4.
【命题意图】本题主要考查函数的极值的概念、导数的运算法则、切线方程、导数应用、等差数列等基础知识,同时考查抽象概括、推理论证能力和创新意识.
【答案】
(Ⅰ)解:当a=1,b=2时,
因为f′(x)=(x-1)(3x-5).
故f′(2)=1.
又f(2)=0,
所以f(x)在点(2,0)处的切线方程为y=x-2.
(Ⅱ)证明:因为f′(x)=3(x-a)(x-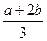 ),
),
由于a<b.
故a<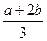 .
.
所以f(x)的两个极值点为x=a,x=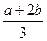 .
.
不妨设x1=a,x2=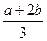 ,
,
因为x3≠x1,x3≠x2,且x3是f(x)的零点,
故x3=b.
又因为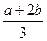 -a=2(b-
-a=2(b-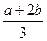 ),
),
x4=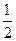 (a+
(a+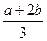 )=
)=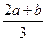 ,
,
所以a,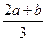 ,
,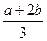 ,b依次成等差数列,
,b依次成等差数列,
所以存在实数x4满足题意,且x4=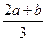 .
.
【点评】本题是一道创新性很强的一道问题,解决此类问题需要灵活的运用所学的知识准确的进行条件之间的转换.另外在解决曲线的切线问题时,要注意曲线“在点p处的切线”是以点P为切点,而“过点P的切线”,点P可能是切点,也可能不是切点,点P可能不在已知的曲线上,切线可能不止一条
(22)(本题满分15分)已知m是非零实数,抛物线C:y2=2px(p>0)的焦点F在直线l:x-my-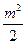 =0上.
=0上.
(Ⅰ)若m=2,求抛物线C的方程;
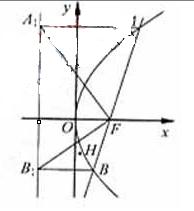
(Ⅱ)设直线l与抛物线C交于A,B两点,过A,B分别作抛物线C的准线的垂直,垂足为A1,B1,△AA1F,△BB1F的重心分别为G,H.求证:对任意非零实数m,抛物线C的准线与x轴的交点在以线段GH为直径的圆外.
【命题意图】本题主要考查抛物线的几何性质,直线与抛物线、点与圆的位置关系等基础知识,同时考查解析几何的基本思想方法和运算求解能力.
【答案】(Ⅰ)解:因为焦点F(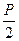 ,0)在直线l上,得
,0)在直线l上,得
p=m2,
又m=2,故p=4.
所以抛物线C的方程为y2=8x.
(Ⅱ)证明:因为抛物线C的焦点F在直线l上,
所以p=m2,
所以抛物线C的方程为y2=2m2x.
设A(x1,y1),B(x2,y2),
由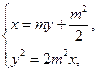 消去x得
消去x得
y2-2m3y-m4=0,
由于m≠0,故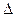 =4m6+4m4>0,
=4m6+4m4>0,
且有y1+y2=2m3,y1y2=-m4,
设M1,M2分别为线段AA1,BB1的中点,
由于2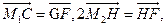
可知G(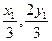 ),H
),H (
(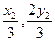 ),
),
所以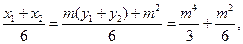
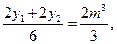
所以GH的中点M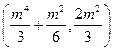 .
.
设R是以线段GH为直径的圆的半径,
则R2=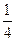
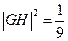 (m2+4)(m2+1)m2.
(m2+4)(m2+1)m2.
设抛物线的准线与x轴交点N(-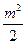 ,0),
,0),
则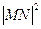 =
=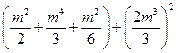
=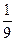 m4(m4+8 m2+4)
m4(m4+8 m2+4)
=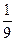 m4[(m2+1)( m2+4)+3m2]
m4[(m2+1)( m2+4)+3m2]
>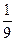 m2 (m2+1)( m2+4)=R2.
m2 (m2+1)( m2+4)=R2.
故N在以线段GH为直径的圆外.
【点评】直线与圆锥曲线相交时解析几何中的一类重要问题,解题时注意应用根与系数的关系及“设而不求”的技巧来解决直线与圆锥曲线的综合性问题.












