非选择题部分(共100 分)
分)
二、填空题:本大题共7小题,每小题4分,共28分。
(11)在如图所示的茎叶图中,甲、乙两组数据的中位数分别是 , .

11.答案45,46
【命题意图】本题主要考查茎叶图的有关知识.
【解析】由题甲的数据分别为28、31、39、42、45、55、57、58、66,其中位 数为45,乙的数据为29、34、35、42、46、48、53、55、67,其中位数为46.
数为45,乙的数据为29、34、35、42、46、48、53、55、67,其中位数为46.
(12)函数f(x)=sin2 (2x-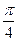 )的最小正周期是 .
)的最小正周期是 .
答案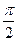
【命题意图】本题主要考查三角恒等变换及三角函数的最小正周期.
【解析】由题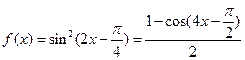
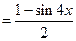 ,所以最小正周期为
,所以最小正周期为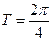
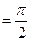 .
.
(13)已知平面向量α,β,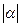 =1,
=1, 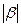 =2,α⊥(α-2β),则
=2,α⊥(α-2β),则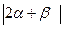 的值是 .
的值是 .
13.答案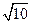
【命题意图】本题主要考查平面向量的基本运算.
【解析】由题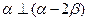 ,所以有
,所以有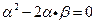 ,因为
,因为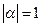 ,
,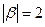 所以
所以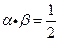 ,由
,由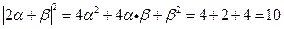
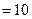 ,所以
,所以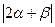 的值为
的值为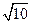 .
.
(14)在如下数表中,已知每行、每列中的数都成等差数列,

那么位于表中的第n行第n+1列的数是 .
14.答案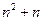
【命题意图】本题主要考查等差数列的有关知识.
【解析】由题,第一列是首项为1,公差为1的等差数列,所以第n行的第一个数为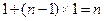 ,由表可得数列的第n行的公差为n,所以第n行的第n+1个数为
,由表可得数列的第n行的公差为n,所以第n行的第n+1个数为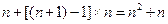 .
.
(15)若正实数x ,y满足2x+y+6=xy,则xy的最小值是 .15.答案18
,y满足2x+y+6=xy,则xy的最小值是 .15.答案18
【命题意图】本题主要考查利用基本不等式求解范围问题.
【解析】由题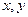 均为正数,
均为正数,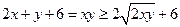 ,令
,令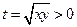 ,则有
,则有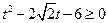 ,解得
,解得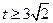 ,即
,即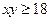 ,所以
,所以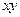 的最小值为18.
的最小值为18.
(16)某商家一月份至五月份累计销售额达3860万元,预测六月份销售额为500万元,七月份销售额比六份递增x%,八月份销售额比七月份递增x%,九、十月份销售总额与七、八月份销售总额相等.若一月至十月份销售总额至少达7000万元,则x的最小值是 .
16.答案20
【命题意图】本题考查二次不等式的实际应用问题,考查学生利用所学知识分析问题解决问题的能力.
【解析】由题知7月份的销售额为500(1+x%),8月份的销售额为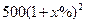 ,所以9月10月份的销售总额为500(1+x%)+
,所以9月10月份的销售总额为500(1+x%)+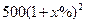 .所以由题可得
.所以由题可得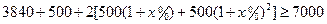 ,令
,令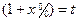 整理可得
整理可得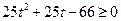 ,解得t的最小值为
,解得t的最小值为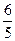 ,所以x的最小值为
,所以x的最小值为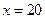 .
.
(17)在平行四边形ABCD中,O是AC与BD的交点,P,Q,M,N分别是线段OA、OB、OC、OD的中点.在A,P,M,C中任取一点记为E,在B,Q,N,D中任取一点记为F.设G为满足向量 的点,则在上述的点G组成的集合中的点,落在平行四边形ABCD外(不含边界)的概率为 .
的点,则在上述的点G组成的集合中的点,落在平行四边形ABCD外(不含边界)的概率为 .
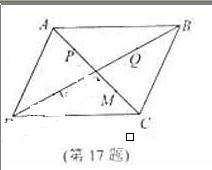
17.答案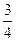
【命题意图】本题主要考查古典概率的有关知识.
【解析】由题可知E总共存在四种可能的位置,F有四种可能的位置,以O为起点,所有的终点 组成的
组成的 基本事件总数为
基本事件总数为
(AD),(AN),(AQ),(AB),(PD),(PN),(PQ),(PB),(MD),(MN),(MQ),(MB),(CD),(CN),(CQ),(CB)共16种,而由平行四边形法则可知满足条件的事件有(AD),(AN), (AQ),(AB) (PB),(PD),(MD),(MB),(CD),(CN),(CQ),(CB)共12种,因此对应的点G构成的集合中点落在平行四边形ABCD的外部的概率为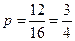 .
.
三、解答题:本大题共5小题,共72分。解答应写出文字说明、证明过程或演算步骤
(18)(本题满分14分)在△ABC中,角A,B,C所对的边分别为a,b,c,设S为△ABC的面积,满足S=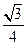 (a2+b2-c2).
(a2+b2-c2).
(Ⅰ)求角C的大小;
(Ⅱ)求sinA+sinB的最大值.
【命题意图】本题主要考查余弦定理、三角形面积公式、三角变换等基础知识同时考查三角运算求解能力.
【答案】(Ⅰ)解:由题意可知
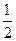 absinC=
absinC=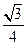 ,2abcosC.
,2abcosC.
所以tanC=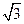 .
.
因为0<C<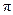 ,
,
所以C=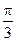 .
.
(Ⅱ)解:由已知sinA+sinB=sinA+sin(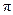 -C-A)=sinA+sin(
-C-A)=sinA+sin(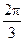 -A)
-A)
=sinA+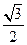 cosA+
cosA+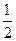 sinA=
sinA=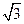 sin(A+
sin(A+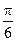 )≤
)≤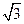 .
.
当△ABC为正三角形时取等号,
所以sinA+sinB的最大值是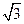 .
.
【点评】在解三角形时,常常将正弦定理、余弦定理结合在一起用,要注意恰当的选取定理,简化运算过程,提高解题速度,痛恨死要注意与平面几何中的有关性质,定理结合起来挖掘题目中的隐含条件.
(19 )(本题满分14分)设a1,d为实数,首项为a1,公差为d的等差数{an}的前n项和为Sn,满足S5S6+
)(本题满分14分)设a1,d为实数,首项为a1,公差为d的等差数{an}的前n项和为Sn,满足S5S6+ 15=0.
15=0.
(Ⅰ)若S5=S.求S6及a1;
(Ⅱ)求d的取值范围.
【命题意图】本题主要考查等差数列的概念、求和公式等基础知识,同时考查运算求解能力及分析问题解决问题的能力.
【答案】
(Ⅰ)解:由题意知S6=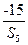 =-3,
=-3,
A6=S6-S5=-8
所以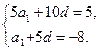
解得a1=7
所以S6= -3,a1=7
(Ⅱ)解:因为S5S6+15=0,
所以(5a1+10d)(6a1+15d)+15=0,
即2a12+9da1+10d2+1=0.
故(4a1+9d)2=d2-8.
所以d2≥8.
故d的取值范围为d≤-2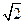 或d≥2
或d≥2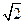 .
.
【点评】等差数列中,通项公式与前n项和公式联系着五个基本量,这五个基本量中,知道其中的三个可以求得另外的两个,往往要解方程或方程组,除掌握这个基本运算关系,还要注意运算中利用等差数列的性质进行整体代换,这样可以简化运算过程.












