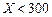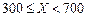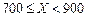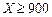20.(本小题满分12分)
根据以往的经验,某工程施工期间的降水量X(单位:mm)对工期的影响如下表:
降水量X |
|
|
|
|
工期延误天数 | 0 | 2 | 6 | 10 |
历年气象资料表明,该工程施工期间降水量X小于300,700,900的概率分别为0.3,0.7,0.9. 求:
(Ⅰ)工期延误天数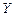 的均值与方差;
的均值与方差;
(Ⅱ)在降水量X至少是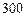 的条件下,工期延误不超过6天的概率.
的条件下,工期延误不超过6天的概率.
考点分析:本题考察条件概率、离散型条件概率分布列的期望与方差。
难易度:★★
解析:
(Ⅰ)由已知条件和概率的加法公式有:
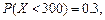
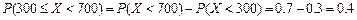 ,
,
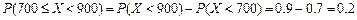 .
.
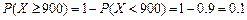 .
.
所以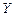 的分布列为:
的分布列为:
| 0 | 2 | 6 | 10 |
| 0.3 | 0.4 | 0.2 | 0.1 |
于是,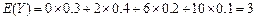 ;
;
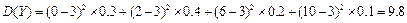 .
.
故工期延误天数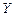 的均值为3,方差为
的均值为3,方差为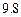 .
.
(Ⅱ)由概率的加法公式,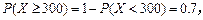
又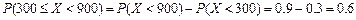 .
.
由条件概率,得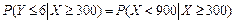
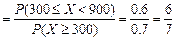 .
.
故在降水量X至少是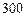 mm的条件下,工期延误不超过6天的概率是
mm的条件下,工期延误不超过6天的概率是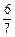 .
.
21.(本小题满分13分)
设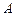 是单位圆
是单位圆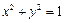 上的任意一点,
上的任意一点,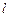 是过点
是过点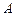 与
与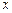 轴垂直的直线,
轴垂直的直线,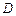 是直线
是直线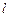 与
与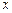 轴的交点,点
轴的交点,点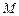 在直线
在直线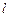 上,且满足
上,且满足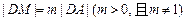 . 当点
. 当点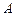 在圆上运动时,记点M的轨迹为曲线
在圆上运动时,记点M的轨迹为曲线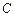 .
.
(Ⅰ)求曲线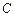 的方程,判断曲线
的方程,判断曲线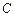 为何种圆锥曲线,并求其焦点坐标;
为何种圆锥曲线,并求其焦点坐标;
(Ⅱ)过原点且斜率为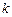 的直线交曲线
的直线交曲线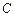 于
于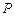 ,
,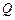 两点,其中
两点,其中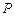 在第一象限,它在
在第一象限,它在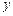 轴上的射影为点
轴上的射影为点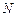 ,直线
,直线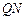 交曲线
交曲线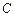 于另一点
于另一点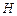 . 是否存在
. 是否存在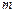 ,使得对任意的
,使得对任意的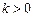 ,都有
,都有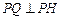 ?若存在,求
?若存在,求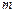 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
考点分析:本题主要考察求曲线的轨迹方程、直线与圆锥曲线的位置关系,要求能正确理解椭圆的标准方程及其几何性质,并能熟练运用代数方法解决几何问题,对运算能力有较高要求。
难易度:★★★
解析:
(Ⅰ)如图1,设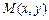 ,
,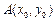 ,则由
,则由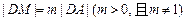 ,
,
可得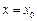 ,
,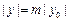 ,所以
,所以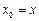 ,
,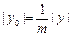 . ①
. ①
因为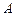 点在单位圆上运动,所以
点在单位圆上运动,所以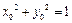 . ②
. ②
将①式代入②式即得所求曲线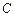 的方程为
的方程为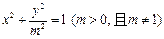 .
.
因为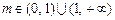 ,所以
,所以
当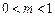 时,曲线
时,曲线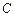 是焦点在
是焦点在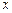 轴上的椭圆,
轴上的椭圆,
两焦点坐标分别为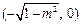 ,
,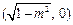 ;
;
当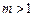 时,曲线
时,曲线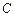 是焦点在
是焦点在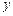 轴上的椭圆,
轴上的椭圆,
两焦点坐标分别为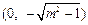 ,
,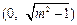 .
.
(Ⅱ)解法1:如图2、3,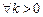 ,设
,设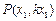 ,
,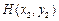 ,则
,则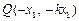 ,
,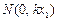 ,
,
直线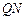 的方程为
的方程为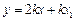 ,将其代入椭圆
,将其代入椭圆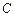 的方程并整理可得
的方程并整理可得
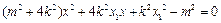 .
.
依题意可知此方程的两根为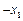 ,
,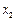 ,于是由韦达定理可得
,于是由韦达定理可得
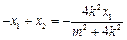 ,即
,即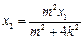 .
.
因为点H在直线QN上,所以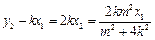 .
.
于是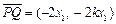 ,
,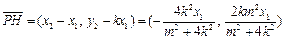 .
.
而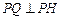 等价于
等价于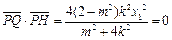 ,
,
即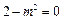 ,又
,又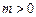 ,得
,得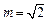 ,
,
故存在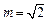 ,使得在其对应的椭圆
,使得在其对应的椭圆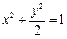 上,对任意的
上,对任意的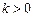 ,都有
,都有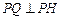 .
.
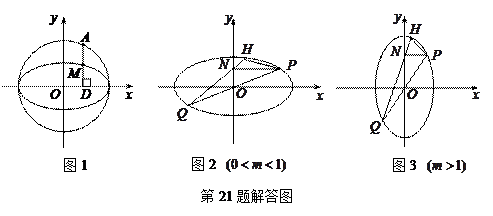
解法2:如图2、3,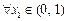 ,设
,设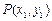 ,
,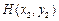 ,则
,则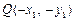 ,
,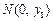 ,
,
因为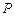 ,
,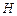 两点在椭圆
两点在椭圆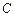 上,所以
上,所以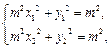 两式相减可得
两式相减可得
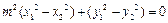 . ③
. ③
依题意,由点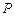 在第一象限可知,点
在第一象限可知,点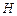 也在第一象限,且
也在第一象限,且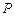 ,
,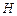 不重合,
不重合,
故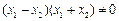 . 于是由③式可得
. 于是由③式可得
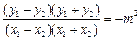 . ④
. ④
又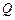 ,
,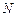 ,
,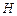 三点共线,所以
三点共线,所以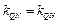 ,即
,即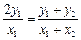 .
.
于是由④式可得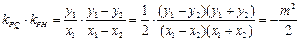 .
.
而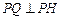 等价于
等价于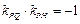 ,即
,即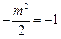 ,又
,又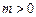 ,得
,得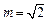 ,
,
故存在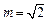 ,使得在其对应的椭圆
,使得在其对应的椭圆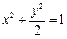 上,对任意的
上,对任意的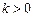 ,都有
,都有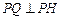 .
.
22.(本小题满分14分)
(Ⅰ)已知函数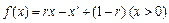 ,其中
,其中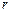 为有理数,且
为有理数,且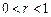 . 求
. 求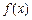 的
的
最小值;
(Ⅱ)试用(Ⅰ)的结果证明如下命题:
设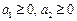 ,
,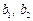 为正有理数. 若
为正有理数. 若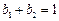 ,则
,则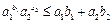 ;
;
(Ⅲ)请将(Ⅱ)中的命题推广到一般形式,并用数学归纳法证明你所推广的命题.
注:当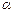 为正有理数时,有求导公式
为正有理数时,有求导公式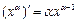 .
.
考点分析:本题主要考察利用导数求函数的最值,并结合推理,考察数学归纳法,对考生的归纳推理能力有较高要求。
难易程度:★★★
解析:(Ⅰ)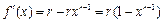 ,令
,令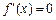 ,解得
,解得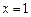 .
.
当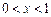 时,
时,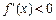 ,所以
,所以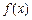 在
在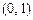 内是减函数;
内是减函数;
当 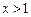 时,
时,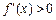 ,所以
,所以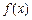 在
在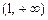 内是增函数.
内是增函数.
故函数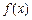 在
在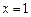 处取得最小值
处取得最小值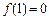 .
.
(Ⅱ)由(Ⅰ)知,当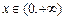 时,有
时,有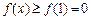 ,即
,即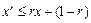 ①
①
若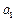 ,
,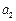 中有一个为0,则
中有一个为0,则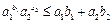 成立;
成立;
若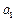 ,
,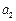 均不为0,又
均不为0,又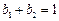 ,可得
,可得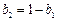 ,于是
,于是
在①中令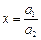 ,
,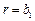 ,可得
,可得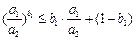 ,
,
即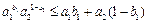 ,亦即
,亦即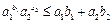 .
.
综上,对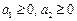 ,
,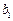 ,
,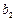 为正有理数且
为正有理数且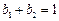 ,总有
,总有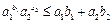 . ②
. ②
(Ⅲ)(Ⅱ)中命题的推广形式为:
设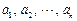 为非负实数,
为非负实数,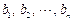 为正有理数.
为正有理数.
若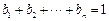 ,则
,则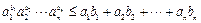 . ③
. ③
用数学归纳法证明如下:
(1)当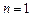 时,
时,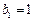 ,有
,有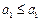 ,③成立.
,③成立.
(2)假设当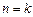 时,③成立,即若
时,③成立,即若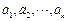 为非负实数,
为非负实数,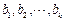 为正有理数,
为正有理数,
且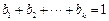 ,则
,则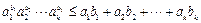 .
.
当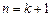 时,已知
时,已知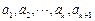 为非负实数,
为非负实数,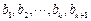 为正有理数,
为正有理数,
且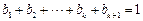 ,此时
,此时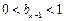 ,即
,即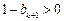 ,于是
,于是
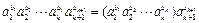 =
=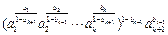 .
.
因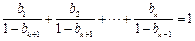 ,由归纳假设可得
,由归纳假设可得
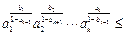
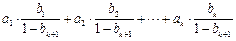
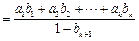 ,
,
从而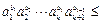
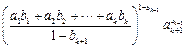 .
.
又因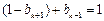 ,由②得
,由②得
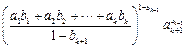
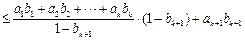
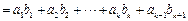 ,
,
从而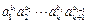
 .
.
故当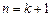 时,③成立.
时,③成立.
由(1)(2)可知,对一切正整数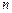 ,所推广的命题成立.
,所推广的命题成立.
说明:(Ⅲ)中如果推广形式中指出③式对成立,则后续证明中不需讨论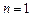 的情况.
的情况.